Chapter 1. Determining a Solubility Product Constant
Discussion
Objectives

- Determine the solubility product constant, Ksp, for calcium iodate by titration of the iodate ion in a saturated solution.
- Become familiar writing equilibrium expressions for slightly soluble salts and be able to interchangeably work between terms of Ksp, concentrations, solubility, and molar solubility.
Introduction
Solubility data is widely used across many disciplines of science, technology and medicine. Engineers use solubility to design water treatment protocols, thereby removing hazardous chemicals from our drinking water. Environmental chemists work to explain and prevent water pollutants by means of careful solubility analyses. Pharmaceutical researchers utilize knowledge of solubility within the body to design drug delivery systems and control drug concentrations in our bloodstream. In this lab we will expand our discussion beyond the solubility rules learned in earlier chemistry courses and become familiar with the extent to which something is soluble. The concepts explored in this lab are fundamental to not only future topics in this course, but also those of other courses and disciplines.
Connection to Lecture
Solubility was discussed in Chemistry 1210 in terms of the solubility rules and that allowed us to classify compounds as soluble and insoluble. In lecture we are learning that there are varying degrees of solubility and it is not so easy to classify a compound as soluble or insoluble. For example PbF2 and SrSO4 are both insoluble according to our solubility rules. However we can determine experimentally that 0.466 g of PbF2 will dissolve in 1 liter of water and 0.092 g of SrSO4 will dissolve in 1 liter of water.
We study solubility equilibria so that we may consider the amount of a compound that will dissolve in a solvent. The solubility product constant, Ksp, is a measure of how much of a solid dissolves to form a saturated solution. Recall from earlier chemistry courses that a saturated solution is a solution in which undissolved solute and dissolved solute are in equilibrium with each other. We can write a chemical equation expressing the equilibrium established between a solid solute and its ions in a saturated solution.
The corresponding solubility product constant, or Ksp, expression is to the right. The Ksp, is the product of molar concentrations of ions raised to the power of their coefficients, analogous to other K expressions we have seen previous in this course.
Question 21.1: Write the solubility equilibrium and the Ksp expression for following slightly soluble salts. a. strontium carbonate
b. lead(II) bromide
c. zinc phosphate
d. silver sulfide
To determine the Ksp for this equation we must know the concentrations of lead and fluoride. However, if we know the concentration of just one ion, by stoichiometry we may determine the concentration of the other ion. We are able to do this because we have a saturated solution; the greatest amount possible of ions in solution are realized and all of these ions in solution come only from the slightly soluble salt. Practically speaking the value of Ksp can be calculated if the concentration of either ion is known, and that is what you will do in this lab.
Question 21.2: A student determines by means of titration that the concentration of fluoride ion is 0.64 M. What is the concentration of lead ions?
Use the [Pb2+] and [F−] to calculate the Ksp of PbF2.
Titration of a Saturated Solution
In this lab you will determine the Ksp for calcium iodate, Ca(IO3)2. To do this you need to find the concentration of either the calcium ions or the iodate ions in a saturated solution. A key concept here is that the solution must be saturated. Recall that the Ksp expression describes the equilibrium between the solid solute and its ions in solution.
In this experiment it is much easier to calculate the concentration of IO3− in solution and this is determined by performing a titration. You have completed several titrations in the laboratory portion of both this and the previous course. Recall that successful titrations require a well-known chemical reaction between the analyte and titrant that goes to completion quickly. This reaction must have a marked change in a property of the solution, which can be used to determine the equivalence point.
To determine the [IO3−] in this titration, the iodate ion will first be reacted with excess iodide ion and acid to produce iodine.
This solution is brown. The iodine will be titrated with a standardized solution of sodium thiosulfate, Na2S2O3.
The titrant, Na2S2O3, has already been standardized for you. The exact concentration to 4 decimals, 0.05xx M, will be printed on the bottle for you to record. You will begin your titration and the solution will turn from brown to yellow. When the yellow color is observed, a starch indicator will be added to signify the end point. Addition of the starch indicator will turn the yellow solution to a blue color from a complex with I2. The end point of the titration occurs when all of the I2 has reacted and is signaled by the disappearance of the blue color.
|
|
The overall stoichiometry for determining the iodate ion concentration by titrating with thiosulfate is shown below:
Data Analysis
The buret will be read once the solution turns colorless, this indicates the end point. Using the volume obtained and the molarity of the thiosulfate from the reagent bottle, the moles of thiosulfate may be collected. Then using the mole ratio from the overall balanced equation, we may find the moles of iodate ion in our solution.
Once we know the moles of our iodate solution, we may simply find the concentration by dividing by the volume of the saturated calcium iodate sample titrated.
We may then calculate the concentration of the calcium ion from the relationship
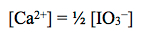
Lastly, using the concentrations of the ions in solution, the Ksp may be calculated using the Ksp expression:
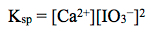
Question 21.3: To determine the solubility product constant (Ksp) at 50°C for Ca(IO3)2, a chemist prepares a saturated solution of the salt at this temperature. They filter and remove a 10.00 mL aliquot of this solution, and add 50.0 mL of distilled water, 2 g of KI and 10 mL of 3 M HCl to the flask. Thiosulfate solution is added to the flask and after 2% starch solution is added it turns blue. The chemist keeps adding thiosulfate solution from the buret until the solution in the flask turns colorless. It takes 14.58 mL of 0.0515 M Na2S2O3 to reach the end point of the titration. The chemical reactions governing the titration are shown above.
a) How many moles of S2O32−(aq) are needed to reach the endpoint of the titration?
b) How many moles of IO3−(aq) reacted to reach the end point of the titration?
c) What is the concentration of lead ions?
d) If 10.00 mL of a the saturated Ca(IO3)2 solution was used, what is the equilibrium concentration of IO3−(aq)?
e) Based on your results from part c), what is the equilibrium concentration of Ca2+(aq)?
f) Write out the Ksp expression for Ca(IO3)2.
g) Determine the Ksp of Ca(IO3)2 at 50°C
Materials Required
- 100-mL graduated cylinder
- 250- and 400-mL beakers
- funnel, filter paper
- ring, clay triangle
- wash bottle
- 2 100-mL beakers
- metal spatula
- 2 stirring rods
- buret, clamp
- 10.00 mL pipet
- 2 250-mL Erlenmeyer flasks
- 10-mL graduated cylinder
- 2 125-mL Erlenmeyer flasks
- stirring motor, stir bar
- 0.2 M potassium iodate, KIO3
- 1 M calcium nitrate, Ca(NO3)2
- standardized 0.05xx M sodium thiosulfate, Na2S2O3
- solid potassium iodide, KI
- 3 M hydrochloric acid, HCl
- vitex starch
- unknown iodate solution, IO3−
- top-loading balance
Cautions
Iodine, formed as an intermediate in the titration, is toxic. Avoid contact with these solutions. Hydrochloric acid is corrosive. If any of these solutions come into contact with your skin or clothing, flood the affected area immediately with water. Goggles must be worn at all times.
Procedure
Answer questions in your lab notebook as you go along. Discussions with your peers and TA are encouraged.
A. Making the calcium iodate saturated solution.
- To prepare the saturated solution of Ca(IO3)2, measure roughly 20 mL of 1 M Ca(NO3)2 into a 250-mL beaker. Next add about 50 mL of 0.2 M KIO3 to the Ca(NO3)2 solution. You should observe a white precipitate. Note: These volume measurements do not need to be exact, so you can use a graduated cylinder to add the solutions to the beaker.
Question 21.4: What is the identity of the white precipitate?
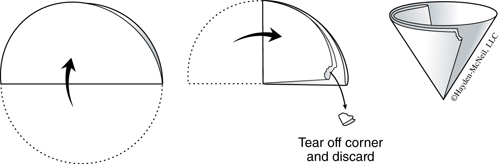
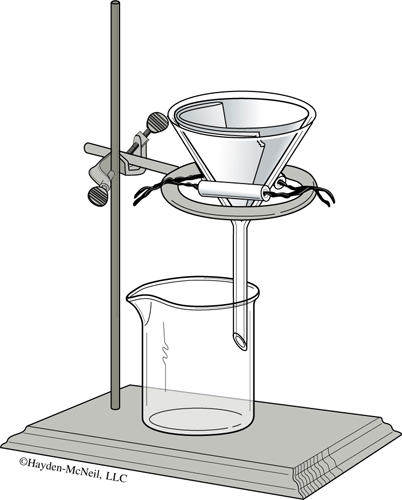
2. Similar to Figure 21.2, assemble a ring, clay triangle, and funnel with filter paper in order to perform a gravity filtration. Fold a piece of filter paper in half, then fold it in half again. In order to fit the filter paper snugly inside the funnel, tear off a small part of the corner as shown in Figure 21.1. Open the filter paper so that one side of the funnel is in contact with a single layer of the filter paper and the other side of the funnel is in contact with three layers of the filter paper. It seems to work best if the side with the tear has three layers. The paper should be in smooth contact with the funnel at the top, but not near the point. Squirting in water with a wash bottle will help keep the filter paper in place.
3. Take the 250-mL beaker from Step 1 and pour as much supernatant liquid through the filter paper as possible, trying your best not to disturb the precipitate. Use a wash bottle filled with distilled water to wash down the sides of the beaker. Swirl the wash water with the solid and quickly pour the mixture on the filter paper. Rinse any remaining solid onto the filter paper with a small amount of water from your wash bottle.
4. Wash the solid Ca(IO3)2 on the filter paper with three small portions of distilled water.
5. Using a microspatula, transfer roughly ⅓ of the wet precipitate to one 100-mL beaker. Leave the left over precipitate on the filter paper. You will only use the precipitate on the filter paper if you mess up one of your trials.
6. Rinse your 100-mL graduated cylinder with distilled water and use it to add 80 mL of distilled water to the beaker containing the wet precipitate.
7. Acquire a stirring motor from the balance room and a stir bar from your TA. Place the stir bar into the beaker containing your 80 mL of water and your Ca(IO3)2 precipitate.
8. Place your beaker on the stirring motor and turn the stirrer on to its lowest speed setting and allow it to stir in order to obtain a saturated solution. While you are waiting for your solution to reach equilibrium complete Part B.
B. Things to do while your solution saturates.
9. Prepare your titration setup: Clean and dry a 250-mL Erlenmeyer flask and label this “titration flask.” Find the 0.05XX M Na2S2O3 on the cart and record its concentration to four decimal places your lab notebook. Label a 250-mL beaker as “standard” and obtain about 75 mL of this solution. Use this solution to rinse a 25-mL buret twice.
10. Clean and dry a funnel and 125-mL Erlenmeyer flask. Label this flask “filtered iodate solution.” Prepare a piece of filter paper as you did in Step 2. Any glassware, as well as the filter paper, must be dry in order to calculate an accurate concentration of IO3–.
11. Prepare a fresh starch solution by adding 0.6 grams of vitex starch to roughly 30 mL of distilled water in a separate 250-mL Erlenmeyer flask; label this flask “starch solution.”
C. Filtering the saturated solution.
12. Filter the saturated solution from Step 8 using the setup you prepared in Step 10. This filtration will be much like the one you did in Step 2. While a saturated solution is necessary to determine the ion concentrations at equilibrium, no solid can be present during the titration.
Question 21.5: What impact would the presence of solid have on your calculated molarity of iodate ions? Hint: Consider your friend Le Châtelier.
D. Titrating the saturated solution.
13. Rinse a 10-mL pipet with two small portions of the saturated Ca(IO3)2 solution. You may discard any rinse solutions down the drain. Pipet 10.00 mL of the saturated solution into the “titration flask” you prepared in step 9.
14. To your “titration flask,” add approximately 50 mL of water using a graduated cylinder and 2 g of solid KI. In addition, add about 10 mL of 3 M HCl and swirl. This is converting all of the IO3−(aq) to I2(aq), which will turn the solution brown.
15. Fill the 25-mL buret you cleaned in Step 9 with 0.05XX M Na2S2O3 and record your initial buret reading. Begin your titration and as the titration proceeds you will observe the brown color of the I2 solution lighten to a more yellow color. When you observe a yellow color stop the titration and add 4 mL of the starch indicator you prepared in Step 11. Notice the color of the solution change to blue.
16. Continue the titration until you reach the endpoint, which is the moment the solution turns colorless. This endpoint indicates all of the iodine has been reacted.
17. Record the buret reading at the endpoint. In your lab notebook, calculate the number of moles of S2O32−(aq) required in the titration using this volume and the molarity recorded from the reagent bottle.
18. Repeat the titration two additional times. If any of the three titrations do not agree to within 0.2 mL, perform another titration.
19. In each trial calculate the moles of iodate ion in the 10.00 mL solution. At the end point what we are observing is the overall reaction:
At the endpoint of the titration:
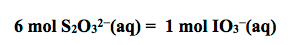
20. Calculate the molarity of IO3− for all three trials. Using the stoichiometry of the ions in solution, calculate the concentration of Ca2+.
21. Calculate the Ksp for Ca(IO3)2 for each trial, the average Ksp and the standard deviation.
Waste Disposal
All solutions may be rinsed down the drain.
Points to Consider
In this lab you are calculating a Ksp from concentration data obtained in the lab. You should compare this value obtained to that reported in the CRC handbook.
- If the Ksp is larger than that in the CRC, what does this tell you about the concentrations you determined?
- If the Ksp is smaller than that in the CRC, what does this tell you about the concentrations you determined?
- Write the equilibrium expression to rationalize your explanation.
- Was there excess precipitate in the solution when you titrated? How would this impact your results?
- What was the temperature of the room? What was the temperature at which the CRC value was determined? How does temperature impact Ksp?